ROB 502: Programming for Robotics: Homework 3
Clicker Questions
Use p4r-clicker to submit your answer
int val1 = 10;
int val2 = 20;
int *b = &val1;
int *c = b;
int **d = &b;
printf("%d\n", **d); // 1
*b = 1;
b = &val2;
printf("%d\n", *b); // 2
printf("%d\n", *c); // 3
printf("%d\n", **d); // 4
*d = &val1;
printf("%d\n", *b); // 5
printf("%d\n", *c); // 6
printf("%d\n", **d); // 7
git pull upstream master
Run the following command to get the updated template file:
git pull upstream master
Problem 1: chase
In this problem we will program one robot (the “chaser”) to chase after another robot (the “runner”).
You have already written the majority of the code needed for this problem, so you should start by copying over all the files you used for homework 2’s braitenberg problem.
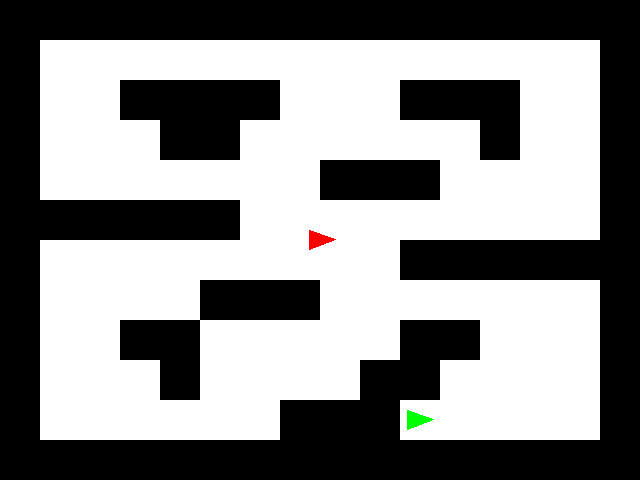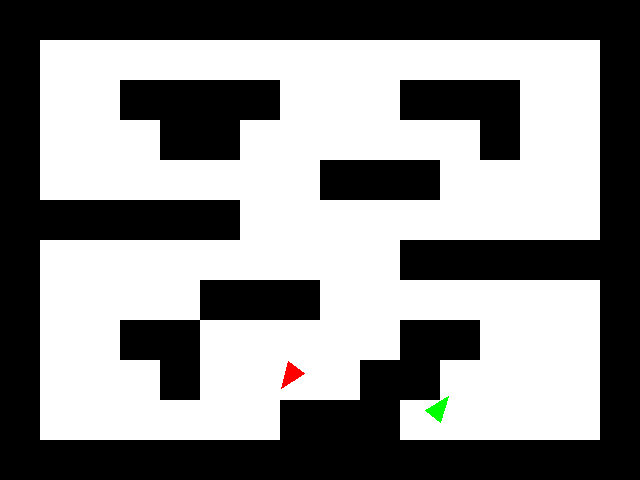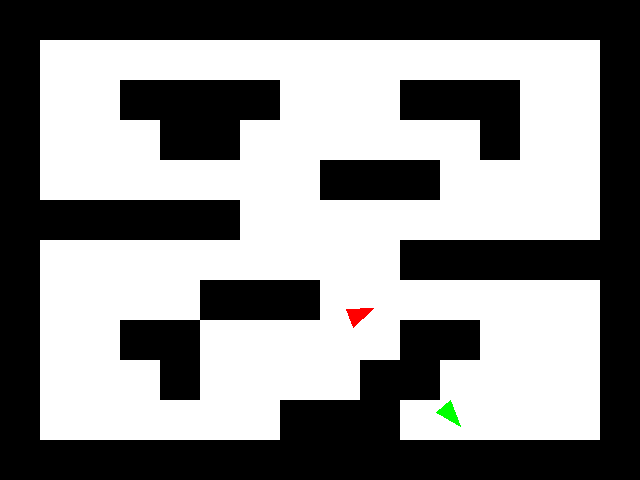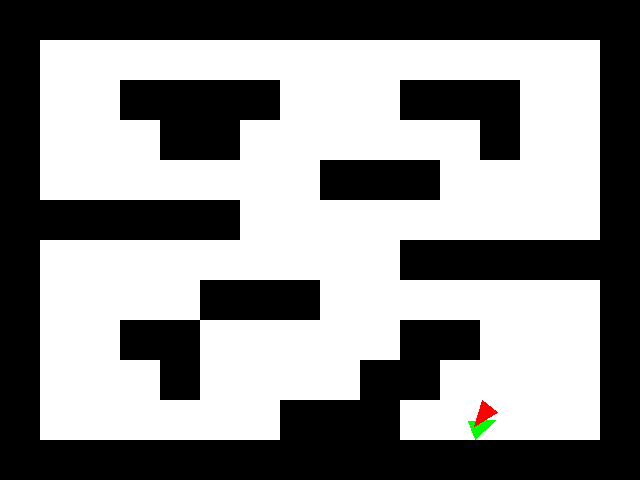
Map setup
Include the following code to specify the map of the environment we are using:
#define WIDTH 640
#define HEIGHT 480
#define BLOCK_SIZE 40
#define MAP "XXXXXXXXXXXXXXXX" \
"X X" \
"X XXXX XXX X" \
"X XX X X" \
"X XXX X" \
"XXXXXX X" \
"X XXXXXX" \
"X XXX X" \
"X XX XX X" \
"X X XX X" \
"X XXX X" \
"XXXXXXXXXXXXXXXX"
#define MAP_W (WIDTH / BLOCK_SIZE)
#define MAP_H (HEIGHT / BLOCK_SIZE)
Wherever there is an X in the map, draw a BLOCK_SIZE by BLOCK_SIZE black square, leaving the remainder of the image white. Modify your previous rectangle function to not center the rectangles. This will make it easier to fit them all on the image.
Draw the chaser robot red, and have it start at the center of the image, pointing to the right.
Add one more command-line argument to your program to accept the map index at which the runner robot should start:
./chase
usage: ./chase <time steps> <fast=0|1|2> <initial runner index>
Draw the runner robot green, and have it start at the center of that map location, pointing to the right.
You can do that like this:
int map_idx_x = initial_runner_idx % MAP_W;
int map_idx_y = initial_runner_idx / MAP_W;
state->runner.x = (map_idx_x + 0.5) * BLOCK_SIZE;
state->runner.y = (map_idx_y + 0.5) * BLOCK_SIZE;
Action model for the robots
The state of each robot can be described by location (x and y), orientation, forward velocity, and angular velocity.
At each time step, the robots have several actions available to them:
- 0: Do nothing
- 1: Increase velocity by 2, capped to a max velocity of 12
- 2: Increase angular velocity by PI / 16 in the counterclockwise direction
- 3: And for the chaser only, increase angular velocity by PI / 16 in the clockwise direction
In addition, angular velocity decays by a factor of 0.8 on each step, and forward velocity is cut in four if the robot has a collision.
In total, movement proceeds like this, first for the chaser and then for the runner:
apply action
theta += angular velocity
angular velocity *= 0.8
move robot by velocity in the theta direction
It is important that the chaser moves first, because its choice is dependent on the runner’s position, and we can’t have the chaser “seeing into the future” of how the runner will be moving on this time step.
After movement for both the chaser and the runner, they resolve collisions, again with the chaser first and the runner second (just to have a defined order). For each robot:
resolve collisions
if robot had any collision with a wall {
velocity *= 0.25 // this can only happen at most once per time step
}
A random-walk for the runner
At every time step, the runner should randomly choose a number from 0 to 19, inclusive. If the number chosen is 1, the runner will take action 1. If it is 2, the runner takes action 2. If it is any other number, the runner takes action 0 (do nothing).
We designed these conditions so that the runner will gradually make interesting trajectories around the map.
Order of collision resolution
In this problem, it is possible for a robot to be in collision with multiple wall blocks simultaneously. When this happens, the robot should only move away from one block by 0.5 pixels (along the from the center of block to the robot center) before moving away from another block. In addition, the blocks should be processed in order of index in the MAP.
For example, if the robot is in collision with the blocks at (5, 7) and (6, 7), we might get the following order of resolutions:
Moving away from block at (5, 7) // collision not fully resolved
Moving away from block at (6, 7) // collision fully resolved
Moving away from block at (5, 7)
Moving away from block at (5, 7) // all collisions fully resolved
The simplest way to deal with this is to effectively have a double-loop structure:
while first time through loop or we had any collisions in the last loop {
for each block in order of low index to high index {
if robot collides with that block {
move 0.5 pixels away from that block
}
}
}
Tree search for the chaser
We are going to program the chaser to “intelligently” select its action at each time step. It is going to do this by searching its actions over a horizon into the future. We will forward simulate the trajectory of the chaser for different possible actions it could take. Then at the end of the simulated trajectory we will compute a score to represent how good of a place we are in relative to the runner. Although we will be simulating multiple steps into the future, we will only ever choose the action that right now would lead to the best outcome. Each time step will perform a complete new search for the best action.
At each time step, the chaser has four possible actions. This means that the number of simulations required to explore all possible sets of actions n steps into the future is 4^n. Unless we reduce this complexity in some way, the chaser will either be very shortsighted or very slow at coming to decisions.
Notice that our actions make changes in velocity. This means that the effects of an action will continue in later time steps even when we choose the “do nothing” action. We will take advantage of this in our forward simulations. After each deliberate action we will automatically perform 3 more “do nothing” actions.
We will use an n of 4, so that our tree search will include a total of 256 different simulations. After each real action choice we have 3 “do nothing” actions, so each simulation will actually be 16 time steps into the future.
We are not simulating the runner’s movements and are assuming the runner stays stationary. This works fine because the runner’s random walk is not trying to get away from the chaser.
Each level of the search will keep track of the following information:
- depth/level of the search
- runner state
- chaser state
The objective function
In order for this search to be effective, we need to be able to evaluate and reward states of the chaser that will actually lead to capturing the runner. The first objective is to minimize the distance between the chaser and the runner at the last timestep of trajectory simulation (i.e., MAX_SEARCH_DEPTH). Unfortunately, by itself this objective is too greedy and sometimes the chaser will get stuck close on the other side of an obstacle from the runner. So for each level of the search we add another term to penalize moving slowly. As long as the chaser keeps on moving around it should eventually find a way to its target!
We want the robot to move at a pace of around 2 pixels per time step, but we don’t want to reward it for going so fast it can’t steer well. We add a term 300 / min(2, chaser velocity) during each level of the search. The 300 is a weight on the term. min(2, ...) keeps the chaser from needing to go faster than 2 pixels per time step, and the division makes it so that the slower the chaser moves, the bigger the penalty (we are trying to minimize the total score). If the chaser velocity is 0, this penalty goes to infinity! Although dividing by zero is often an error, here we know that it will go to infinity, and that this simply means “really really bad,” and won’t cause any problems.
The code will look something like:
search_actions() {
if chaser collides with runner {
return a score of 0
}
if depth >= max depth {
return a score of distance-between-chaser-and-runner
}
for each chaser action {
make a new copy of the search state to modify
simulate this action forward (movement and collisions)
as long as the chaser and runner aren't colliding,
simulate 3 more "do nothings" forward (movement and collisions)
score = search_actions(new search state, with depth + 1)
score += 300 / min(2, chaser velocity)
}
return the best/lowest score of any action, and which action that was
}
I actually use the following function signature:
double search_actions(search_node_t node, int *chosen_action);
Notice that I pass the search_node_t by value so that each recursive call automatically gets its own copy to modify. Also notice that I use a pointer int *chosen_action to return the final chosen action:
*chosen_action = whatever my best action is;
The function itself returns the best score possible for any action deeper in the tree search.
Optimization
So that your code runs fast enough for the auto-grader, you will want to submit your final code compiled with -O3 optimization and with -fsanitize=address disabled/commented out.
You will also want to be intelligent about calculating collisions between the map and robots, because performing the full collision check between the robots and every single wall block will be inefficient.
The simplest way to do this will be to only consider the nine “tiles” around the robot’s current position. My favorite way to do this is to first find which “block x” and “block y” the robot is at, and then to do a double loop around these. By block x/y, I mean the coordinates that can index MAP and that have a total MAP_W and MAP_H.
int robot_block_x = ...;
int robot_block_y = ...;
for (int dy = -1; dy <= 1; dy++) {
for (int dx = -1; dx <= 1; dx++) {
int block_x = robot_block_x + dx;
int block_y = robot_block_y + dy;
...
}
}
Evaluation
At each time step, you should print out a line with the runner action first and then the chaser action. Your code will be run with a maximum of 400 time steps, but it should stop after the runner has been caught/collided with. Your code will pass each test as long as the sequence of actions you list ends with catching the runner, in 400 time steps or fewer. This means you are welcome to experiment with making changes to the method described above. On the other hand, the method described should work without changes.
Here are some interesting initial runner locations to try: 19, 170, 126
./chase
usage: ./chase <time steps> <fast=0|1|2> <initial runner index>
./chase 1000 2 19
0 1
0 2
0 2
0 2
0 1
0 1
0 1
0 0
0 0
1 1
In addition to the “fast mode 1” from last time, we also have introduced a new “fast mode 2”. In fast mode 2, do not call image_server_start at all! Otherwise it is like fast mode 1. Your code will be evaluated in fast mode 2 and this will prevent bind(): Address already in use errors between multiple image servers being evaluated at the same time.
Note that because we are testing your action outputs here and not the visual output, in “fast” mode, your code does not need to have a 1 second delay at the end. You may either remove the delay entirely, or shorten the delay such that the animation viewer still works for you to see the final state.